2.1.2 The greenhouse effect
The atmosphere is nearly transparent to visible light, absorbing about 20% of the incoming solar radiation. As a consequence, the majority of the absorption takes place at Earth's surface (see section 2.1.6). On the other hand, the atmosphere is almost opaque across most of the infrared part of the electromagnetic spectrum. This is related to the radiative properties of some minor constituents of the atmosphere, especially water vapour, carbon dioxide, methane and ozone. Those gases constitute only a small fraction of the atmospheric composition, while the two dominant components (molecular nitrogen and oxygen, see section 1.2.1) play nearly no part in this opacity. Nevertheless, a significant fraction of the energy emitted by the Earth's surface is absorbed by the atmosphere and re-emitted, significantly increasing the temperature of the system.
In a garden greenhouse, panes of glass are transparent to visible light but opaque to infra-red radiation, "trapping" part of the energy emitted by the surface and resulting in a warming of the air. By analogy, the alteration of the energy budget by some minor atmospheric constituents described above is called the greenhouse effect and those minor constituents the greenhouse gas. However, the climate system is much more complex than a greenhouse and in a garden greenhouse a significant fraction of the warming is related to the reduction of the turbulent heat exchanges with atmosphere, not in the modification of the radiative fluxes. The analogy should be used with caution.
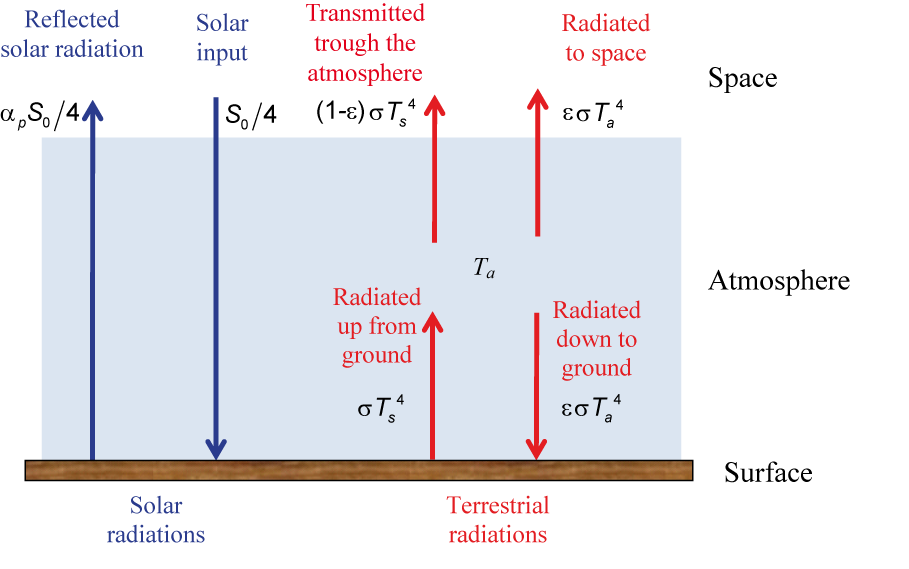
The greenhouse effect can be illustrated by a very simple model in which the atmosphere is represented by a single homogenous layer of temperature Ta, totally transparent to the solar radiation and totally opaque to the infrared radiations emitted by the Earth's surface (Fig. 2.4). Because of this opacity of the atmosphere to surface radiation, all the energy radiated to space is from the atmosphere. Using Eq. (2.3), the balance at the top of the atmosphere is thus:
In this simple model, Ta is thus equal to Te, the effective emission temperature of the Earth. At the Earth's surface, the balance between the energy emitted by the surface, and the incoming solar fluxes, and the infra-red flux coming from the atmosphere gives:
Combining (2.5) and (2.6) leads to
| (2.8) |
Because of the greenhouse effect, the surface temperature is thus much higher than Te, reaching 303 K (30°C) in this example. This temperature is actually higher that the observed mean surface temperature of 288 K (15°C) because of some strong crude approximations made in this simple model.
.png)
|
We can improve our model by taking into account the fact that the atmosphere is not a perfect blackbody (Fig. 2.5). Using the emissivity of an object () (which is defined as the ratio of energy radiated by this object to energy radiated by a black body at the same temperature), we can write the budget at the surface as:
The emissivity is also equal to the fraction of the radiation that is absorbed by the object. The fraction being transmitted through the object is thus equal to (1-) and the balance at the top of the atmosphere is:
Eqs. (2.9) and (2.10) lead to:
| (2.11) |
| (2.12) |
For =0, corresponding to an atmosphere totally transparent to infra-red radiations Ts = Te, which is well in agreement with the result of section 2.1.1. For a perfect blackbody, we get a result identical to Eq. (2.7), as expected. A typical value of 0.97 for the atmosphere provides a value of TS = 1.18Te, i.e. 301 K (28°C). We can also compute Ta as:
| (2.13) |
|




