3.3.2 Ocean
The major equations that govern the ocean dynamics are based on the same principles as the equations for the atmosphere. The only significant difference is that the equation for the specific humidity is not required for the ocean, while a new equation for the salinity needs to be introduced. The equation of state is also fundamentally different. Unlike the atmosphere, there is no simple law for the ocean and the standard equation of state is expressed as a function of the pressure, the temperature and the salinity as a long polynomial series.
It is much easier to compute the heating rate in the ocean than in the atmosphere. In addition to the heat exchanges at the surface, the only significant heat source in the ocean is the absorption of solar radiation. This is taken into account in the model through an exponential decay of the solar irradiance. The situation for salinity is even more straightforward, as there is no source or sink of salinity inside the ocean. The equations governing these two variables are thus relatively simple:
where Fsol is the absorption of solar radiation in the ocean. Eq. 3.10 does not apply to the in situ temperature, but the potential temperature in order to account for the effect of the compressibility of seawater. The difference between those two temperatures is relatively low in the upper ocean, but it can reach several tenths of a degree in the deeper layers, an important signal in those areas where the gradients are relatively small (see section 1.3.3.2).
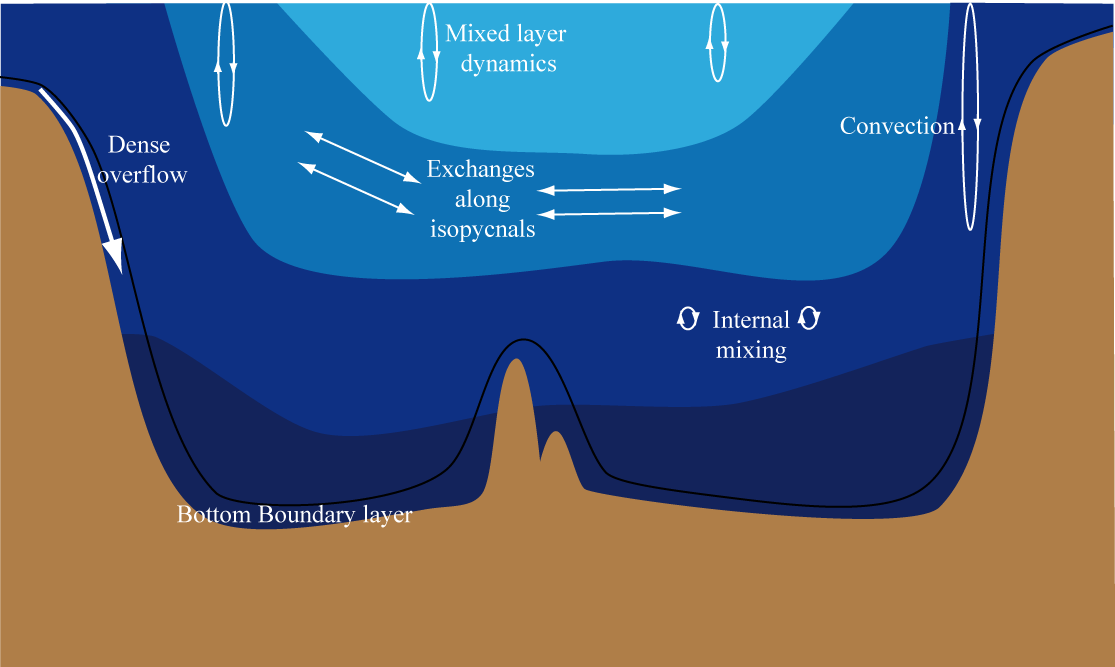
In Eqs. 3.10 and 3.11, in contrast to section 3.3.1, we have explicitly added a term to the right hand side representing the influence of the processes at scales that cannot be included in the model. As small-scale processes tend to mix properties, they are generally modelled as a diffusion term Fdiff. In its simplest form, a Laplacian formulation is retained. This is also often the formulation selected for the friction term (in Eq. 3.4). Because of the very different scales of ocean model grids on the vertical (a few hundred meters) and on the horizontal (tens to hundreds of kilometres), the small-scale processes in these two directions have different properties. As a consequence, the coefficients associated with the Laplacian (diffusion coefficient, and viscosity for tracer and momentum equations, respectively) differ by several orders of magnitude in the vertical and the horizontal. Actually, it appears that, rather than separating horizontal and vertical directions, it is better to use a referential that is aligned with the density surfaces. To this end, isopycnal (along surfaces of equal density) and diapycnal (normal to surfaces of constant density) diffusion coefficients are calculated. These coefficients can be simply chosen, or they can be computed using sophisticated modules (including turbulence models) that take into account the stirring of the winds, the influence of density gradients, the breaking of surface and internal waves, etc.
However, all small-scale processes cannot be represented by a diffusion term. For instance, dense water formed at high latitudes can flow down the slope in narrow boundary currents called overflows. They have a strong influence on the water mass properties but could not be represented on the model grid scale. In this case, a parameterization of their effects as a transport process rather than a diffusion term appears more appropriate.
|




