3.2.1 Energy balance models

As indicated by their name, energy balance models estimate the changes in the climate system from an analysis of the energy budget of the Earth. In their simplest form, they do not include any explicit spatial dimension, providing only globally averaged values for the computed variables. They are thus referred to as zero-dimensional EBMs. The basis for these EBMs was introduced by both Budyko (1969) and Sellers in (1969). Their fundamental equation is very similar to those analysed in sections 2.1.1 and 2.1.5:

Changes in heat storage = absorbed solar radiation - emitted terrestrial radiation

where, as in section 2.1.5.2, C_E is the effective heat capacity of the media (measured in J m^-2 K^-1), T_s the surface temperature, t the time, ${\alpha }_p$ the planetary albedo, S₀ the Total Solar Irradiance (TSI) and A$\uparrow$ the total amount of energy that is emitted by a 1 m² surface of the Earth. A$\uparrow$ could be represented on the basis of the Stefan-Boltzmann law, using a factor ${\tau }_a$ to represent the infrared transmissivity of the atmosphere (including the greenhouse gas effect), as

where $\epsilon$ is the emissivity of the surface. Using an albedo of 0.3, and an emissivity of 0.97, a value of ${\tau }_a$ of 0.64 leads to an equilibrium temperature T_s = 287K, which is close to the observed one. In some EBMs, Eq. (3.2) is linearised to give an even simpler formulation of the model. On the other hand, ${\tau }_a$ and ${\alpha }_p$ are often parameterised as a function of the temperature, in particular to take into account the fact that cooling increases the surface area covered by ice and snow, and thus increases the planetary albedo.

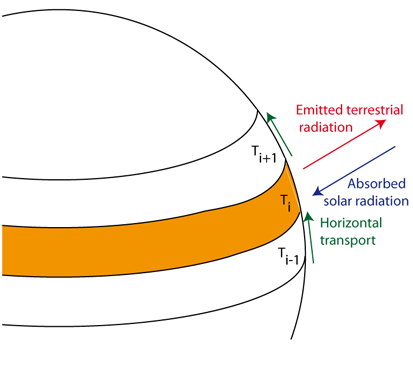
In order to take the geographical distribution of temperature at the Earth’s surface into account, zero-dimensional EBMs can be extended to include one (generally the latitude) or two horizontal dimensions (Fig. 3.3). An additional term $\Delta \mathrm{transp}$ is then included in Eq. 3.1 representing the net effect of heat input and output associated with horizontal transport:

An index i has been added to the surface temperature to indicate that the variable corresponds to the region i. The simplest form for the transport is to treat it as a linear function of temperature, but more sophisticated parameterisations are also used, including, for instance, a diffusion term.

Box models have clear similarities to EBMs as they represent large areas or an entire component of the system by an average which describes the mean over one “box”. The exchanges between the compartments are then parameterised as a function of the characteristics of the different boxes. The exact definition of the boxes depends on the purpose of the model. For instance, some box models have a compartment for the atmosphere, the land surface, the ocean surface layers and the deep ocean, possibly making a distinction between the two hemispheres. Others include additional components allowing a description of the carbon cycle and thus have boxes corresponding to the various reservoirs described in section 2.3.

---