4.1.4 Transient response of the climate system
Because of the thermal inertia of the Earth (see section 2.1.5), the equilibrium response described in section 4.1.3 is only achieved when all the components of the system have adjusted to the new forcing. It can take years or decades for the atmosphere, and centuries or millennia for the seas and the ice sheets, to reach this new equilibrium.
Following the same approach as in sections 4.1.1 and 4.1.3, we will assume that the thermal inertia can be represented at the first order by a slab with homogenous temperature Ts and heat capacity Cs. Using the same notation as for Eq. 4.4, the energy balance of the system can be written as:
If we assume that the radiative forcing Q is equal to zero for t<0 and is constant for t0, this equation can easily be solved, leading to:
When t is very large, we obtain, as expected, the equilibrium solution described by Eq. 4.5. represents a timescale, and when t=, the temperature change has reached 63% of its equilibrium value. is dependent on the heat capacity of the system Cs and on the strength of the feedbacks. This implies that with larger values of (-1/) (i.e. grater climate sensitivity) the time taken to reach equilibrium will be longer. This is an important characteristic of the climate system, which also holds when much more sophisticated representations of the climate system than the one shown Eq. 4.14 are used.
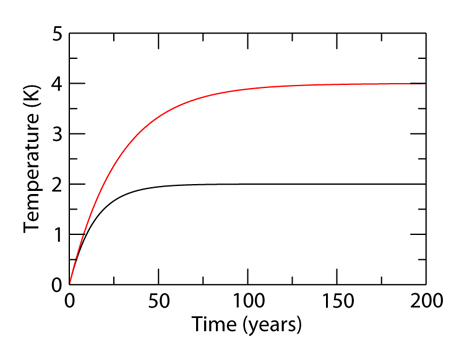
This behaviour can be clearly illustrated by an example (Fig. 4.8). Let us choose for the climate sensitivity values of 2 and 4°C (equivalent to values of equal to -1.9 and -0.95 Wm-2K-1, respectively), a heat capacity corresponding to a depth of 200 meters of water distributed over the whole globe (Cs = 4180 103 x 200 = 8.36 108 JK-1m-2) and a radiative forcing corresponding to a doubling of the CO2 concentration in the atmosphere (Q= 3.8 Wm-2). As expected, the two different climate sensitivities produce a factor two between the equilibrium responses. However, during the first 15 years, the two curves are virtually identical. It can easily be demonstrated that the slope of the curve at t = 0 is independent of the climate sensitivity. As a consequence, knowing the temperature changes in the years immediately following the application of the perturbation does not necessarily provide clear information on the long term evolution of the system. This is one of the reasons why the magnitude of future climate change is still uncertain, even though several decades worth of observations of global warming are already available (see Chapter 6).
The long adjustment of the climate system to the forcing has led to the definition of the transient climate response (TCR), which is defined by the IPCC as the global average of the annual mean temperature change averaged over the years 60 to 80 in an experiment in which the CO2 concentration is increased by 1% per year until year 70 (by which time it is double its initial value). The TCR values derived from models are generally between 1.4 and 2.5°C (Randall et al. 2007). The uncertainty on TCR is thus smaller than the ones of the equilibrium climate sensitivity, because TCR is more constrained by recent changes in temperature.
Before closing this section, it is important to mention that some changes can be classified as either forcing or response depending on the particular focus of the investigator. For instance, in a study of glacial-interglacial climate changes, the building of ice sheets is generally considered as a response of the system to orbital forcing, implying powerful feedbacks (see Chapter 5). On the other hand, if an investigator is mainly interested in atmospheric and oceanic circulation during glacial periods, the ice sheets could be treated as boundary conditions and their influence on the Earth's radiative balance (in particular through their albedo) as a radiative forcing. This distinction between forcing and response can, in some cases, be even more subtle. It is thus important in climatology, as in many other disciplines, to define precisely what we consider the system we are studying to be, and what are the boundary conditions and forcings.
|
|
Applet 4.1: Temperature changes obtained as a solution of 4.14. |




