G
Geostrophic equilibrium
In the atmosphere and the ocean, on a large scale and away from the boundaries (surface, coast) and the equator, the dominant terms in the horizontal equation of motion are the Coriolis force and the force due to the horizontal pressure gradient. The geostrophic balance, which assumes a balance between those two forces, is thus a reasonable approximation:
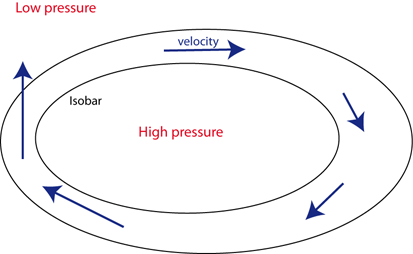
In this equation p is the pressure, the density, f the Coriolis parameter and ug, vg the components of (geostrophic) velocity in the two horizontal directions. f equals 2sin , where is the Earth's angular velocity and the latitude. f is positive in the Northern Hemisphere and negative in the Southern Hemisphere. When this balance is achieved, the fluid is said to be in geostrophic equilibrium and, knowing the horizontal pressure distribution, the horizontal velocity can be computed. The geostrophic equilibrium explains why the flow is clockwise around a high pressure in the Northern Hemisphere, and anticlockwise around a low pressure.
|
Glacier
A glacier is a mass of ice that originates on land, and usually has an area larger than 0.1 km2. See section 1.4.1.
Glacial inception
The glacial inception is the start of a glacial period characterised by an increase in the volume of the ice sheets. See section 5.4.
Gradient
The gradient of a scalar field is a vector that points in the direction of the greatest increase of the scalar field and whose magnitude is proportional to the rate of change. The gradient of f(x,y,z) denoted grad(f), f or f is defined by:
The projection of the gradient over one direction is often called the gradient in this direction. For instance f/z is often called the vertical gradient of f.
Greenhouse gas
A greenhouse gas is a gas that has an impact on the radiative properties of the atmosphere by its ability to absorb radiation in specific infrared wavelengths, leading to the greenhouse effect. See section 2.1.2.
Grid
The numerical resolution of the equations governing the development of the
climate system generally
requires the definition of a grid, whose nodes correspond to the locations where the model variables
are computed. The values computed at these nodes provide enough information to reconstruct, over the
whole domain, an approximation of the corresponding field (such as the temperature). An important
characteristic of a grid is its spatial resolution, which is related to the distance between two
different values computed by the model.
See sections 3.1.1 and 3.4.2.
|
Gulf Stream
The Gulf Stream is a strong current found along the southeast coast of the USA. The current is manly wind driven and forms the western boundary of the subtropical gyre in the Atlantic. To the general public, the Gulf Stream also means the whole northern branch of the subtropical gyre, including the North Atlantic Drift. As the Gulf Stream transports warm water northward, its path is associated with relatively high temperatures compared to other oceanic regions at the same latitude. However, rather than stressing the climate role of the Gulf Stream, it is more appropriate to analyse the oceanic heat transport associated with the wind driven and thermohaline circulations, both of which contribute to the Gulf Stream mass transport. In particular, the thermohaline circulation in the Atlantic contributes to the relative mild conditions found in Europe. Nevertheless, the main reason for the different winter temperatures in Eastern Canada and Western Europe is the atmospheric circulation that brings relatively warm air of oceanic origin to Europe. See sections 1.3.2 and 2.1.5.2.
Gyres
Gyres are quasi-circular patterns of circulation in the ocean. For instance, the subtropical gyres are almost closed loops of ocean currents present at latitudes between roughly 15 and 45o. See section 1.3.2.




