Levermann et al. (2009) have proposed a minimal conceptual model for the abrupt monsoon transitions that have been reconstructed for the Holocene and the last glacial period on the basis of various paleoclimate observations.
Precipitation and wind speed as a function of the radiative flux
Changing the parameter $l$ may lead to a small time delay before the figures adjust to the new values.
Conceptual models are designed to investigate easily the role played by different processes in complex systems. Abrupt monsoon transitions seem to have occurred in the past in response to a relatively weak external forcing. This suggests that positive feedbacks may have amplified the response of the system to a small signal. The model proposed by Levermann et al. (2009) illustrates the fundamental role for monsoons of the moisture-advection feedback in which a larger transport of moisture from the cold ocean to the warm land induces a latent heat release over land that amplifies the temperature differences and thus the circulation.
The model relies on the conservation of heat and moisture of a volume over land of length $L$ and of vertical extent $H$. It focuses only one the rainy season of the annual monsoon cycle.
Geometry of conceptual model and fundamental moisture-advection feedback. The same notation as in the text is used for wind $W$, precipitation $P$, net radiative influx $R$, vertical scale $H$ and horizontal scale $L$. Arrows in the feedback loop indicate the amplification of one physical processes by another. Figure from Levermann et al. (2009).
|
|
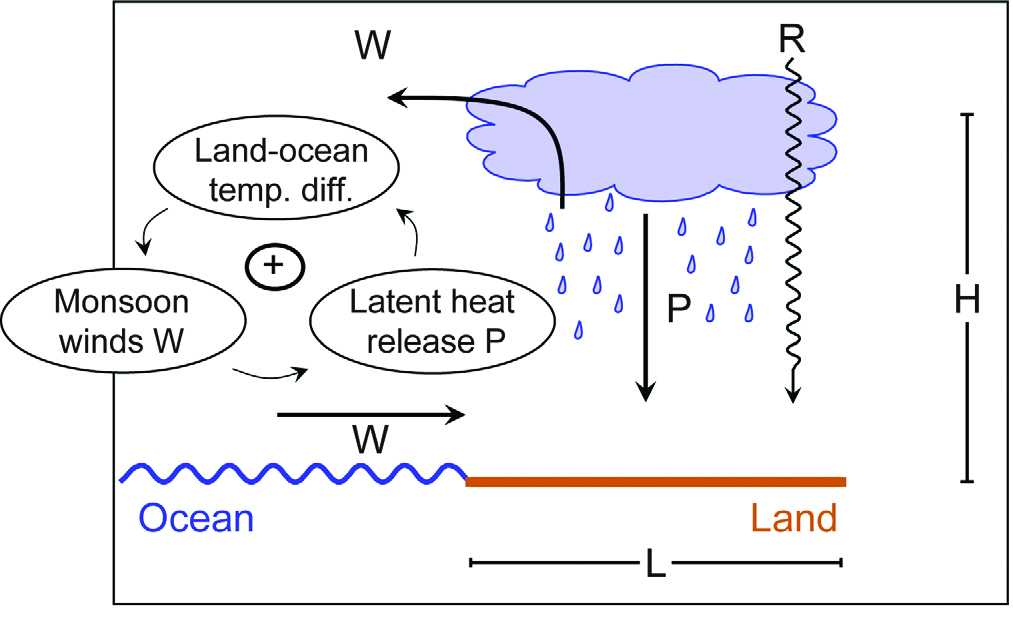
The heat balance equation is
|
$$ {\sp 1.2em \sc L.P \sp 1.2em}↙{⏟}↙\text"latent heat release"-{\sp 1.2em εC_pW.\ΔT \sp 1.2em}↙{⏟}↙\text"heat transport divergence"+{\sp 1.2em R \sp 1.2em}↙{⏟}↙\text"relative heating"=0$$
|
(1) |
where $\sc L$ is the latent heat of condensation (J kg$^{-1}$), $P$ is the mean precipitation over land (kg m$^{-2}$ s$^{-1}$). $C_p$ is the volumetric heat capacity of air at constant pressure (J m$^{-3}$ K$^{-1}$), $W$ is the landward mean wind speed (ms$^{-1}$), $\ΔT$ is the atmospheric temperature difference between land and ocean (K) and $R$ is the net radiative influx (Jm$^{-2}$s$^{-1}$). Here $R$ is generally negative because of the net radiative loss of the atmospheric column. $ε$, the ratio between horizontal and vertical scales ($L$/$H$) is introduced as heat transport is applied on the lateral boundaries of the box while latent heat realease and radiative heating are proportional to its horizontal surface.
The mass-balance equation is
|
$$ {\sp 1.2em εW.ρ(q_O-q_L) \sp 1.2em}↙{⏟}↙\text"moisture flow from ocean to land"-{\sp 1.2em P \sp 1.2em}↙{⏟}↙\text"precipitation"=0$$
|
(2) |
where $q_O$ and $q_L$ are the specific humidity over ocean and land, respectively, and $ρ$ is the mean air density (kg m$^{-3}$).
Based on observational evidences and theoretical considerations (for details see Lvermann et al., 2009). It is assumed that $W=α.\ΔT$ and $P=βq_L$, where $α$ and $β$ are parameters that can be estimated from observations. These two linear relationships, when included in Eq. (1) and (2), lead to the dimensional governing equation of the model:
|
$$ W^3+β/{ερ}W^2-α/{εC_p}(\sc L q_O β+R).W-{αβ}/{ε^2ρC_p}.R=0$$
|
(3) |
The introduction of non-dimensional variables $w≡Wερ/β$ and $p≡P/(q_Oβ)$ provides the non-dimensional equation
|
$$ w^3+w^2-(l+r)w-r=0$$
|
(4) |
where $r$ is the dimensionless radiative influx, $r≡R.εαρ^2$/$(C_pβ^2)$, and $l$ is a measure of the relative role of latent and advective heat transport, $l≡(\sc L q_O β)$/$(C_pβ^2$/$αρ^2$)). The solutions $w(r)$ of Eq. (4) depends on the parameter $l$ which determines a critical threshold of the radiative flux ($r_c$) below which no physical solution exists. This corresponds to a critical value for the dimentionless wind ($w_c$) and precipitation ($p_c$). Precipitation is directly related to wind speed as $p=w/{1+w}$.
The solutions $w(r)$ of Eq. (4) corresponds to the roots of a cubic polynomial and they are determined entirely by a choice of the parameter $l$.
In order to answer the questions in the following quiz, you can modify the parameter $l$ of the model and identify its effect on the non-dimensional wind $w$ and precipitation $p$. After answering each question, please check it using the box on the left before going to the next question.
Levermann A., J. Schewe, V. Petoukhov, and H. Held (2009). Basic mechanism for abrupt monsoon transitions. Proceedings of the National Academy of Sciences, 106(49):20572–20577, doi: 10.1073/pnas.0901414106.
Schewe J. , A. Levermann and H. Cheng (2012). A critical humidity threshold for monsoon transitions, Clim. Past, 8, 535-544, doi:10.5194/cp-8-535-2012.
